Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutritionGiven mathf(x)2f(1x)=x^22\tag 1/math Setting mathx=1x/math then we get mathf(1x)2f(11x)=(1x)^22/math mathf(1x)2f(x)=x^22x3/math math2f\\int \frac{{x}^{\frac{1}{2}}}{{(1x)}^{\frac{1}{2}}} \, dx\ > <

If F X X 1x 1 Then F 2x In Terms Of F X Is
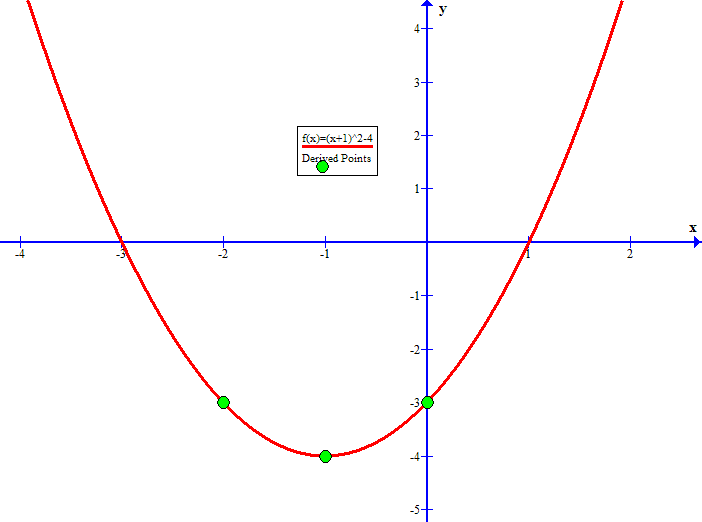
F(x)=(x-1)^2 graph
F(x)=(x-1)^2 graph- The domain is x in RR The range is y in (0,1 The denominator is =1x^2 AA x in RR, 1x^2>0 Therefore, The domain of f(x) is x in RR To determine the range, proceedFind the Derivative g(x)=(e^x)/(x^21) Differentiate using the Quotient Rule which states that is where and Differentiate using the Exponential Rule which states that is where =




Quadratische Funktionen Parabel 1 5 Aufgaben Fit In Mathe
You evaluate "f (x)" in exactly the same way that you've always evaluated "y" Namely, you take the number they give you for the input variable, you plug it in for the variable, and you simplify to get the answer For instance Given f (x) = x 2 2x – 1, find f (2)Deriveringsregler för produkter och kvoter (Observera att derivering av produkter och kvoter inte är så enkelt som derivering av summor och differenser, där man kan derivera funktionsuttrycken termvis, dvs var för sig!) D(xsinx) =1 sinxx cosx=sinxxcosx D(xlnx−x)=1 lnxx x1 −1=lnx1−1=lnxExtended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition
Så f(x) = ln(a x) er (også) en stamfunktion til 1 / xDet betyder, at der findes et tal k, så ln(a x) = ln(x) kSætter vi x = 1, ser vi, at ln(a) = ln(1) k = kAltså er ln(a x) = ln(a) ln(x) Vi har nu den fundamentale regneregel for logaritmer ln(a b) = ln(a) ln(b) ♦ Af ln(a) = ln(b a/b) = ln(b) ln(a / b) ser vi, at ln(a / b) = ln(a) – ln(b) ♦ Funktionen f (x) = x^4 − 4x^3 − x^2 har en eller flera minimipunkter Bestäm denna/dessa Hej! Edited pfb on Accepted Answer pfb x= For y=x^3 4x^2 1 your plot command will be variant of plot (x,y) Sign in to answer this question
In mathematics, For the multiplicative inverse of a real number, divide 1 by the number For example, the reciprocal of 5 is one fifth (1/5 or 02), and the reciprocal of 025 is 11 Example 1 f(x) = x We'll find the derivative of the function f(x) = x1 To do this we will use the formula f (x) = lim f(x 0 0) Δx→0 Δx Graphically, we will be finding the slope of the tangent line at at an arbitrary point (x 0, 1 x 1 0) on the graph of y = x (The graph of y = x 1 is a hyperbola in the same way that the graph of Hej,Jag har ett problem som jag inte kan hitta någon lösning påLåt f(x) = x^2 5 Beräkna f(f(0)) Hur ska




Transformations Of The 1 X Function Video Lesson Transcript Study Com




If F X Be Defined On 2 2 And Is Given By F X 1 2 X 0 X 1 0 X 2 And G X F X F X Find G X
When f (x) = x 4 2x 3 3x 2 ax b is divided by x 1 and x 1, we get remainders 19 and 5 respectively Find the remainder when f(x) is divided by x 3 The zeroes of a polynomial are values of x in a polynomial that makes the polynomial equal to zeroSnabbfakta Skärmstorlek 27 " Upplösning 19 x 1080 Bildförhållande 169 Anslutning DisplayPort, HDMI Paneltyp IPS Ljusstyrka för bild 250 cd/m² Uppdateringsfrekvens 75 Hz Ergonomi Höjd, Lutning, Pivot (rotation), Vridbar bas VESAmått 100 x 100 mm TCOcertifierad Ja Färg Svart ENERGY STARcertifierad Ja Inbyggda enheter USB hubb Energiklass Klass DDomain of f(x) = x/(x^21) Natural Language;




Quadratische Funktionen Parabel 1 5 Aufgaben Fit In Mathe




Ex 13 1 24 Find Lim X 1 Where F X X 2 1 X 1 X 2 1
Rationella uttryck Räkning med algebraiska uttryck som innehåller bråk liknar till stor del vanlig bråkräkning Multiplikation och division av bråkuttryck följer samma räkneregler som gäller för vanliga bråktal, ba c d = a c b d och c d ba = b ca d Exempel 8 3x x−y 4x 2xy = 3x 4x (x−y) (2xy) = 12x2 (x−y) (2xy)Examples and CounterExamples Examples 3 • f(x) = 3x−5 is 1to1 • f(x) = x2 is not 1to1 • f(x) = x3 is 1to1 • f(x) = 1 x is 1to1 • f(x) = xn −x, n > 0, is not 1to1 Proof • f(x 1) = f(x 2) ⇒ 3x 1 − 5 = 3x 2 − 5 ⇒ x 1 = x 2In general, f(x) = ax−b, a 6= 0, is 1to1Graficar f(x) = −2x 2 3x – 3 a = −2, por lo que la gráfica abrirá hacia abajo y será más delgada que f(x) = x 2 c = −3, por lo que se moverá a intersectar el eje y en (0, −3) Antes de hacer la tabla de valores, observa los valores de a y c para tener una idea general de cómo debe quedar la gráfica
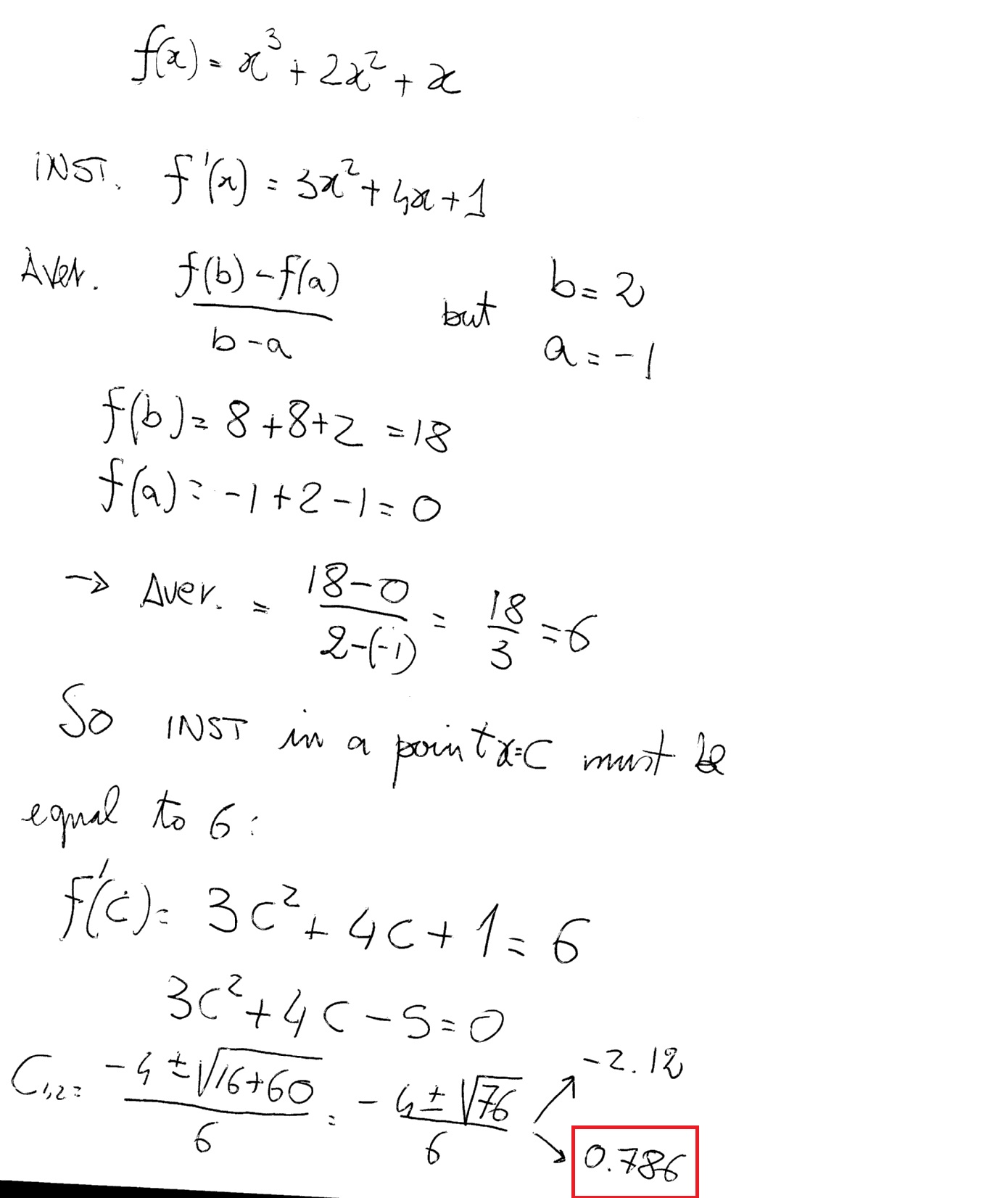



If F Is Defined By F X X 3 2x 2 X How Do You Find The Value Of X When The Average Rate Of Change Of F On The Interval X 1 To X



Berechne Die Nullstellen Fur Die Funktion F F X 1 2x X 2 Mathelounge
What are the critical points of the function f(x) = x2/x²1?MontiA Hej Behöver hjälp med att rita graferna för a) f(x)= x^2 4 b) f(x)= 2^xDivide f2, the coefficient of the x term, by 2 to get \frac{f}{2}1 Then add the square of \frac{f}{2}1 to both sides of the equation This step makes the left hand side of
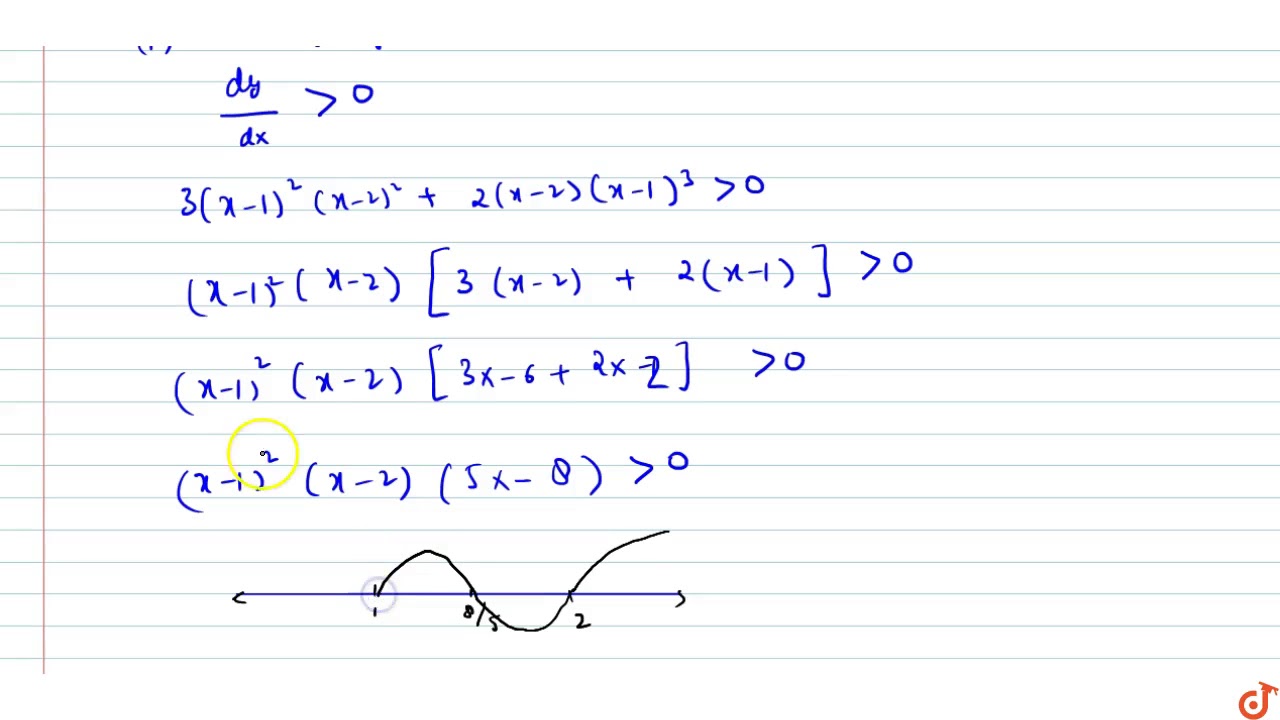



Find The Intervals In Which F X X 1 3 X 2 2 Is Increasing Or Decreasing Youtube




Quadratic Function Wikipedia
Calculus Derivatives Limit Definition of Derivative 1 AnswerJag tänker på videoklippet och exempel 2 F(x) x^2 1 Jag kan se att det kommer bli en "glad mun på grafen" men sen vet jag inte mer hur grafen ska ritas, hur ser man det?Steps for Solving Linear Equation f ( x ) = 1 \frac { 2 } { x 1 } , s f ( x) = 1 − x 1 2 , s Multiply both sides of the equation by x1 Multiply both sides of the equation by x 1 fx\left (x1\right)=x12 f x ( x 1) = x 1 − 2 Use the distributive property to multiply fx by x1
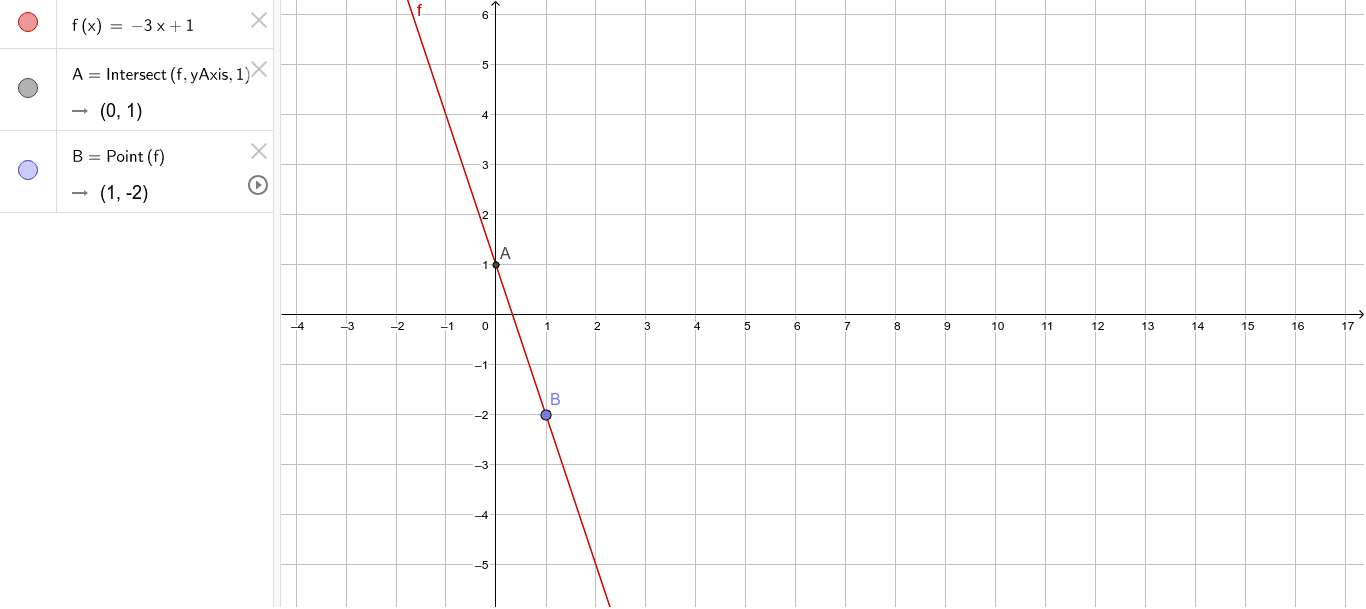



F X 3x 1 Geogebra



What Is F X And G X If F 2x 1 G X 1 X And F 2x 1 2g X 1 2x 2 Is Satisfied Quora
So applying a function f and then its inverse f1 gives us the original value back again f1 ( f(x) ) = x We could also have put the functions in the other order and it still works f( f1 (x) ) = xGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!~126~ 由圖形來判別微分與連續: (1)函數圖形上的斷點:不連續的點。 (2)函數圖形上的斷點、尖點、跳躍點或跳動很厲害的點:不可微分的點。 (練習12) 設f(x)= ≠ 0 , 0, 0 1 sin x x x x ,請問f(x)在x=0 連續嗎?可微分嗎? Ans:f 在x=0 連續但不可微分。 綜合練習 1 (1)設f(t)表速度函數,t為時間,則
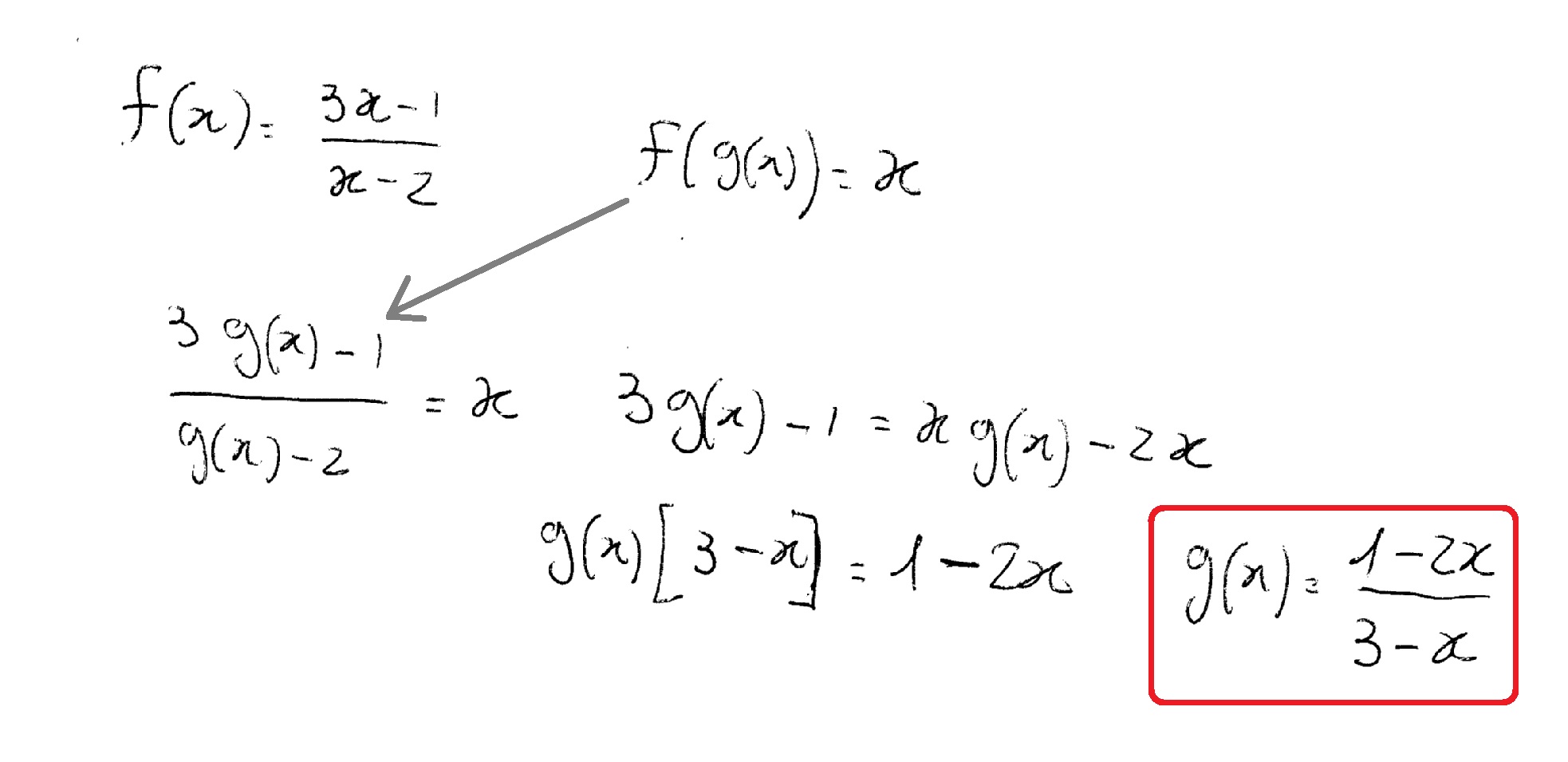



Let F X 3x 1 X 2 And F G X X How Do You Find G X Socratic



Http Www Ruhr Uni Bochum De Imperia Md Content Mathematik Lehrstuhlxiii Eti L05 Pdf
Symbolen f(x) Ni har förmodligen sett den här symbolen någon gång förut Det är ett annat sätt att skriva en funktion y=2x3 kan också skrivas f(x)=2x3 Då vi vill veta värdet på funktionen så sätter vi in et värde på x Om vi vill veta vad funktionen f(x)=2x3 får för värde då x=4 så skriver vi så här f(4)=2Beteckningen f (x) och algebraiska uttryck f (x) är en förkortning för "funktionen som beror på variabeln x" f (x) är alltså samma sak som funktionens formel Man brukar därför säga att y = f (x) då yvärdet ges då vi sätter in x – värdet i formeln I tidigare videos harHärledning f' (x)=e^x I det förra avsnittet visade vi att det finns ett tal e, med den speciella egenskapen att om f (x)=e x så har denna funktion derivatan f ´ (x)=e x I det här avsnittet ska vi visa att derivatan av f (x)=e x faktiskt är f' (x)=e x, genom



Www Math Kit Edu Iana1 Lehre Hm108w Media Hm1 11 Loe Pdf
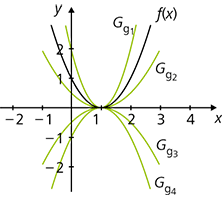



Form Und Lageanderungen Von Funktionsgraphen Analysis Einfach Erklart
PLEASE UPVOTE if you find this helpful THANK YOU The critical points of a function are the points at which the derivative equals zero or is undefined Assuming f(x) = (x2)/(x²1) f'(Försöker att lösa den här uppgiften nu, jag lyckades komma fram till att jag har tre punkter 0, 2 och 5 Ex 13, 1 Deleted for CBSE Board 22 Exams Ex 13, 2 Deleted for CBSE Board 22 Exams Ex 13, 3 (i) Important Deleted for CBSE Board 22 Exams You are here Ex 13, 3 (ii) Ex 13 , 4 Deleted for CBSE Board 22 Exams



Www2 Klett De Sixcms Media Php 229 Ls By 12 K2 Le 1 3 Pdf



Www2 Hs Esslingen De Sigg Vorlesungen Aufgaben Mathe1 Diff 2 Pdf
Ableitung (hSchreibweise) von f (x)=1/x 2 Ich kriege es einfach nicht hin und hoffe, dass ihr mir schnell helfen könnt Ich soll die Ableitung der Funktion f (x)=1/x^2 in der hSchreibweise aufstellen Vielen Dank schonmal im VorausThe points (x,y,z) of the sphere x 2 y 2 z 2 = 1, satisfying the condition x = 05, are a circle y 2 z 2 = 075 of radius on the plane x = 05 The inequality y ≤ 075 holds on an arc The length of the arc is 5/6 of the length of the circle, which is why the conditional probability is equal to 5/6Examples 2 f(x) = X∞ k=0 (−1)kx2k = 1−x2 x4 −x6 ··= X∞ k=0 (−x2)k = 1 1−(−x2) = 1 1x2, for x < 1 f(x) = X∞ k=0 x2k1 3k = x 1 3 x3 1 9 x5 1 27 x7 ··= x X∞ k=0 x2 3 k = x 1−(x2/3) = 3x 3−x2 for x2/3 < 1 12 Radius of Convergence Radius of Convergence There are exactly three possibilities for a




Let F X 0 If X Lt 0 X If 0 X 1 2 X If 1 Chegg Com



Zeichnen Sie Die Funktion F X 1 2 X 2 1 X 3 Mathelounge
Let f(x) = {(1 cos 4x)/x2, if x < 0 and a, if x = 0 and √x/(√(16 √x) 4), if x > 0} If f(x) is continuous at x = 0, determine the value of aThus, x 2/3 = 1 so that and x = 1 or x = 1 In addition, note that f ' is NOT DEFINED at x =0 To avoid using a calculator, it is convenient to use numbers like x = 8, 1/8, 1/8, and 8 as "test points" to construct the adjoining sign chart for the first derivative, f 'I de punkter där funktionen g är nollskild och där den har en derivata, är derivatan av kvoten f/g funktionen ′ = ′ ′Bevis Börja med att beräkna derivatan av funktionen 1/gDerivatan av en sammansatt funktion och vetskapen att derivatan av 1/x är 1/x 2, ger att ′ = ′Därmed kan produktregeln användas för att räkna ut derivatan av f(x)/g(x)
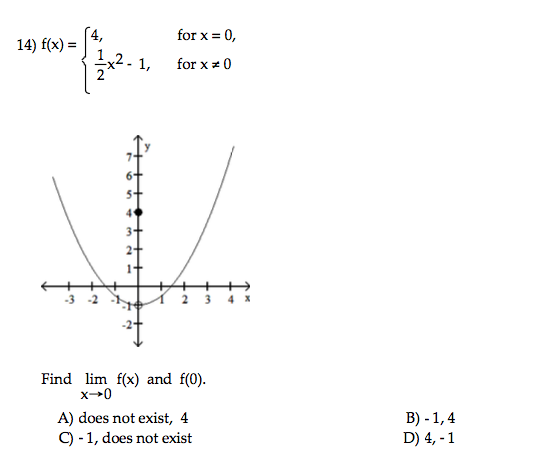



F X 4 For X 0 1 2 X 2 1 For X Notequalto 0 Chegg Com




Bijection Function F X Y X Y 1 2x 2y 2 Mathematics Stack Exchange
関数 y=f (x) の逆関数が存在するためには,関数 y=f (x) は 1対1の関数 でなければならない. 高校で扱う関数で言えば,「 単調増加関数 」または「 単調減少関数 」がこれに対応する. 逆関数の性質 ある関数 y=f (x) のグラフとその逆関数 f 1(x) とは y=xExempel 5 Vi tittar nu på funktionerna f(x) = och g(x) = 4 – x 2 och hittar definitionsmängden samt värdemängden för de sammansatta funktiorna Vi måste uppenbarligen begränsa värdet inom kvadratroten till enbart poritiva tal Därför kan sen sammansatta funktionen f(g(x)) = enbart anta positiva värden av den inre funktionen g(x) = 4 – x 2Get an answer for 'Differentiate (x^21)/(x^21)?' and find homework help for other Math questions at eNotes




If The Function F X X 2 1 X 1 When X 1 K When X 1




Finding Inverse Functions Quadratic Example 2 Video Khan Academy
17 Inverse Functions Notation The inverse of the function f is denoted by f 1 (if your browser doesn't support superscripts, that is looks like f with an exponent of 1) and is pronounced "f inverse" Although the inverse of a function looks like you're raising the function to the 1Given f (x) = 3x 2 – x 4, find the simplified form of the following expression, and evaluate at h = 0 This isn't really a functionsoperations question, but something like this often arises in the functionsoperations contextMath Input NEW Use textbook math notation to enter your math Try it




Wertetabelle X 0 0 5 1 Y F X X 2 0 0 25 1 Graph Der Funktion Pdf Kostenfreier Download




Maximum Value Of Function F X Frac X 4 X 2 X 6 2x 3 1 When X 1 Mathematics Stack Exchange
由圖形來判別微分與連續: (1)函數圖形上的斷點:不連續的點。 (2)函數圖形上的斷點、尖點、跳躍點或跳動很厲害的點:不可微分的點。 O x 例題3 設f(x)= ≠ 0 , 0, 0 1 sin x x x x ,請問f(x)在x=0 連續嗎?可微分嗎? Ans:f 在x=0 連續但不可微分。 (練習1) 設f(x)= ≠ 0 , 0, 0 1 2 sin x x x x$$ f(x)=x^{2}5$$ Nu har vi alltså regler för hur vi bestämmer primitiva funktioner till potensfunktioner och exponentialfunktioner Vi vet också att det går att använda villkor för att hitta en specifik primitiv funktion (att bestämma konstanttermen)Example 2 f(x) = x n where n = 1, 2, 3 d In this example we answer the question "What is x n ?" Once we know the dx answer we can use it to, for example, find the derivative of f(x) = x4 by replacing n by 4 At this point in our studies, we only know one tool for finding derivatives – the difference quotient




Let F X 1 X On 1 3 Find L F P And U F P When P 1 2 3 Mathematics Stack Exchange



View Question What Is F 2 If F X 1 2x
Domain of f(x) = x/(x^21) Natural Language;X = x 1, x = x 2, , x = x k, where x 1, x 2, , x k are roots of Q(x) To find the vertical asymptotes of f(x) be sure that it is in lowest terms by canceling any common factors, and then find the roots of Q(x) 3 Oblique Asymptotes The rational function f(x) = P(x) / Q(x) in lowest terms has an oblique asymptote if the degree ofSummary "Function Composition" is applying one function to the results of another (g º f) (x) = g (f (x)), first apply f (), then apply g () We must also respect the domain of the first function Some functions can be decomposed into two (or more) simpler functions
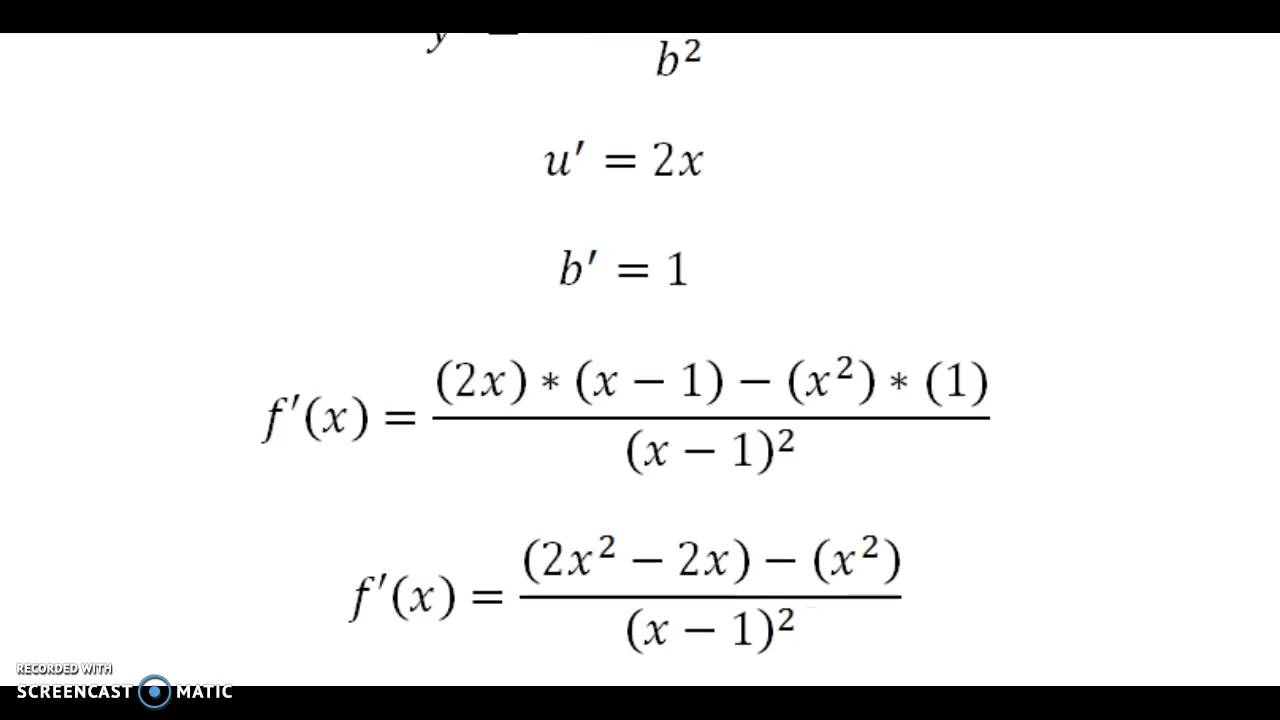



Derivada De Un Funcion F X X 2 X 1 Youtube




Normale Matheguru
52 Uniform convergence 59 Example 57 Define fn R → R by fn(x) = 1 x n)n Then by the limit formula for the exponential, which we do not prove here, fn → ex pointwise on R 52\displaystyle x_1 x_2\quad\Rightarrow\quad f(x_1) \ge f(x_2)\,\mbox{} Med vardagligt språk säger alltså definitionen av tex växande funktion att för ett x värde till höger på x axeln är funktionsvärdet minst lika stort som för ett x värde till vänster How do you find the derivative of #f(x)=1/x^2# using the limit process?




If F X X 2 1 X 2 Then Find The Value Of F X F 1 X Maths Relations And Functions Meritnation Com




Solution If F X 1 1 X 2 Then What Is F X



Math Scene Equations Iii Lesson 3 Quadratic Equations



What Is The Minimum Value Of F X X 1 X 2 X 3 Quora
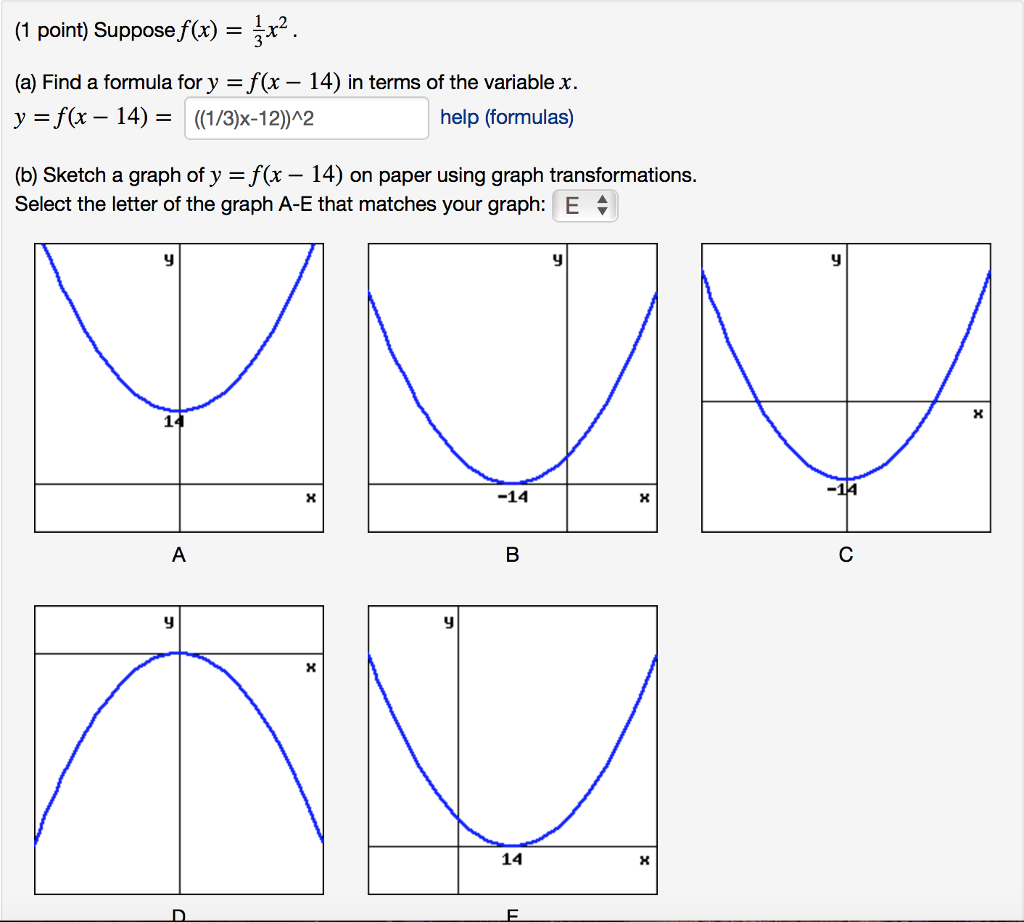



Suppose F X 1 3 X 2 A Find A Formula For Y Chegg Com



The Function F R Gt 1 2 1 2 Defined As F X X 1 X 2 Is Youtube



Http Www Ruhr Uni Bochum De Imperia Md Content Mathematik Lehrstuhlxiii Eti L08 Pdf



Discuss Continuity Of The Function F Given By F X X 1 X 2 At X 1 And X 2 From Mathematics Continuity And Differentiability Class 12 Cbse



F X X



Solution Hello How Do I Graph F X X 2 1 X 1 What Does Lim X Gt 1 X 2 1 X 1 Equal I Graphed The Function With A Discontinuity At X 1 But I 39 M Not Sure How My Second Questio



Wie Zeichne Ich Die Funktion F X 1 X Mathelounge




O Grafico Que Melhor Representa A Funcao Real F X 1 2 X Brainly Com Br




Find The Points Of Local Maxima Or Local Minima And The Corresponding Local Maximum And Minimum Values Of The Following Function F X X 1 3 X 1 2 Mathematics Topperlearning Com 3agvvkgg




If F X X 1x 1 Then F 2x In Terms Of F X Is




Let F 1 2 Infinity 3 4 Infinity Where F X X 2 X 1 Find The Inverse Of F X Hence Or Otherwise Solve The Equation X 2 X 1 Maths Relations And Functions Meritnation Com




Suppose F X X 1 2 What Is F X F X 1 2x Chegg Com



Biomath Transformation Of Graphs



Math Scene Equations Iii Lesson 3 Quadratic Equations




Najti F 1 2 F X X 1 X 2 3 F X 2x 1 2x 1 4 F X 2x 1 7x5 F X 2x 3 5 4x Shkolnye Znaniya Com




Wertetabelle X 0 0 5 1 Y F X X 2 0 0 25 1 Graph Der Funktion Pdf Kostenfreier Download




If F X 2x 1 If X Gt 1 And X 2 1 If 1 Lt X Lt 1 And If F 1 F 3 F X F 2 F Youtube




F X X 1 X To F 2 Shkolnye Znaniya Com
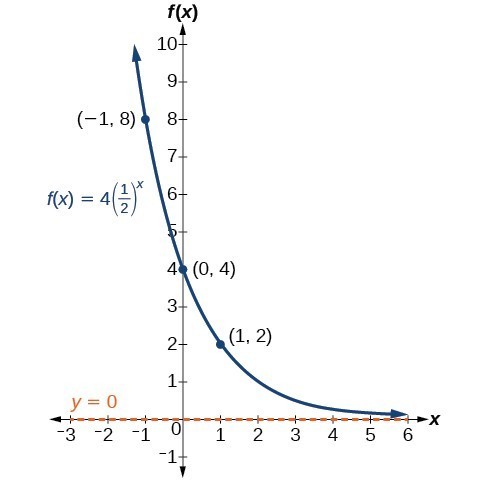



Graph Exponential Functions Using Transformations College Algebra



Gegeben Sei Die Funktion F Mit F X 1 3 X 3 3x 2 8x 1 A Bestimme F 4 Mathelounge



F X 1



Find The Values Of P And Q So That F X X2 3x P Ifx 1 Qx 2 Ifx 1 Is Differentiable At X 1 Studyrankersonline



Stammfunktion F Von F X X 1 X 1 Bestimmen Mit F 1 2 Mathelounge



Www M2 Ma Tum De Foswiki Pub M2 Allgemeines Einfnumsose11twoinone Blatt 1 Pdf



How Do You Graph Y X 1 2 4 Socratic




Lp Potenzreihen Und Taylor Entwicklung



F X Ax 2 Geogebra



F X X Graph



Form Und Lageanderungen Von Funktionsgraphen Analysis Einfach Erklart



F X 1 X 2 Graph




Which Of The Following Represents Graph Of F X 1 2 X Brainly Com




14 Grafica De Las Funciones F X 1 E X F X 1 2 X Download Scientific Diagram



Was Ist Bei Dieser Ableitung Falsch F X 1 X E 1 2 X 2 Mathelounge




Wertetabelle X 0 0 5 1 Y F X X 2 0 0 25 1 Graph Der Funktion Pdf Kostenfreier Download
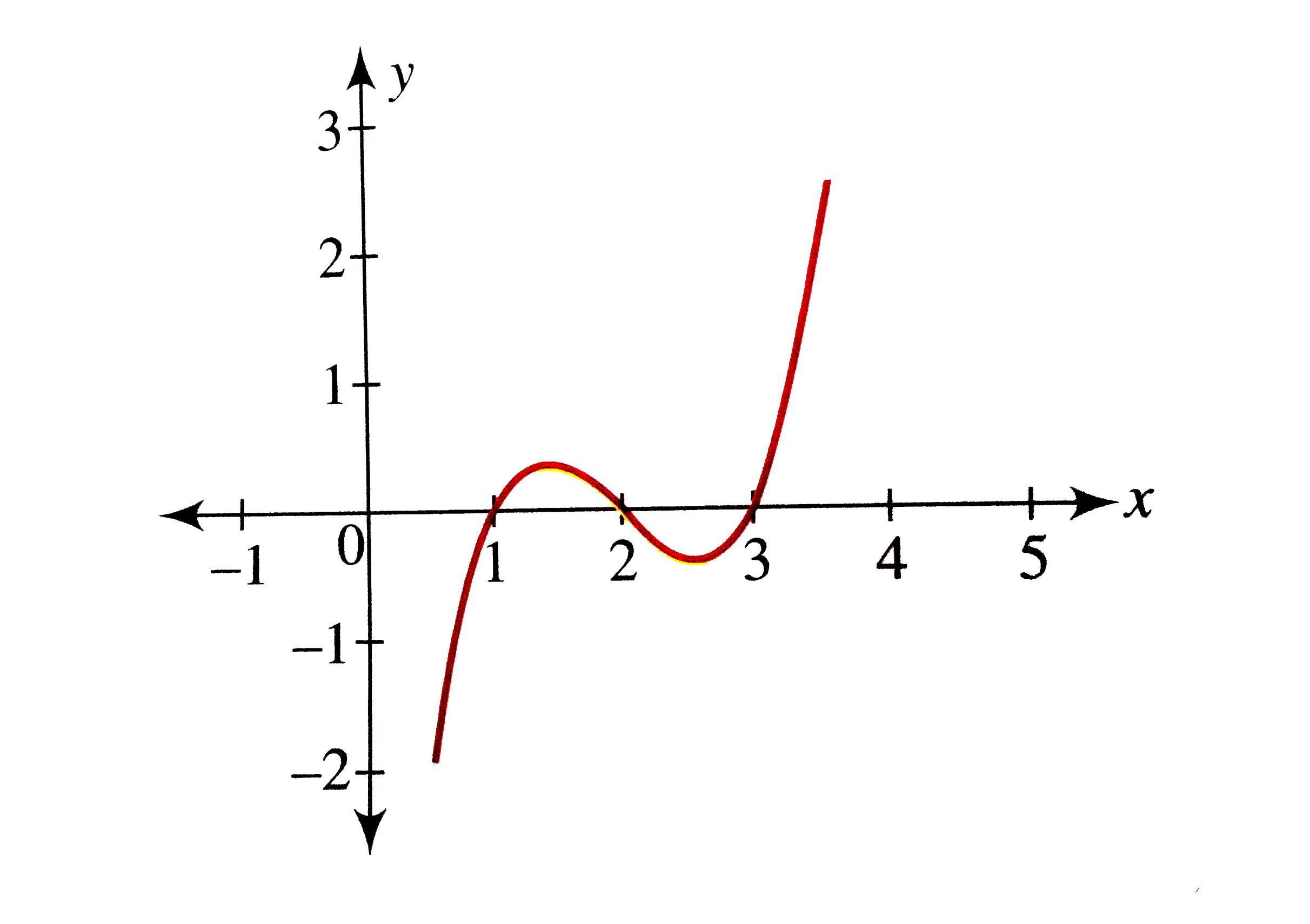



Draw The Graph Of F X X 1 X 2 X 3



Www3 Math Tu Berlin De Vorlesungen Ss07 Analysis2 Nachklausurloesung Pdf




If X 1 A N D F X X 1 X 1 Is A Real Function Then F F F 2 Is A 1 B 2 C 3 D 4




Was Ist 4 Wurzel X 1 2 X 3 Aufgeleitet Mathe Mathematik Stammfunktion
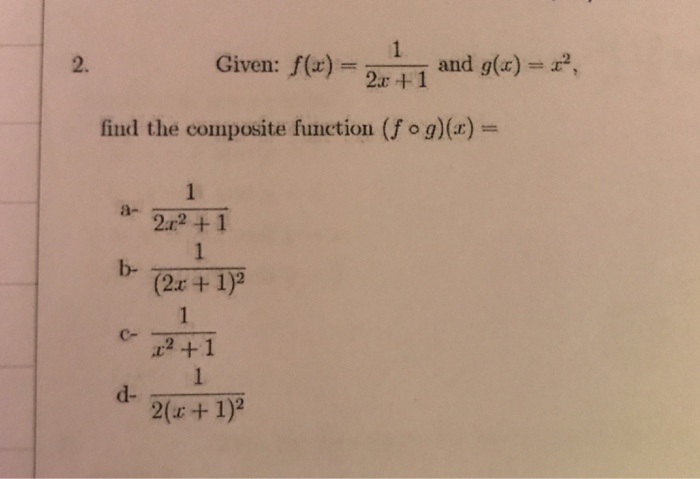



Given F X 1 2x 1 And G X X 2 Find The Chegg Com




Quadratic Function Wikipedia




Misc 6 Let F X X2 1 X2 X R Find Range Chapter 2




How To Tell If A Function Is Even Or Odd 8 Steps With Pictures




If F X X 1 X 2 X 3 Then A Maximum Value Of F X Is 3 If X In 2 3 B Maximum Youtube
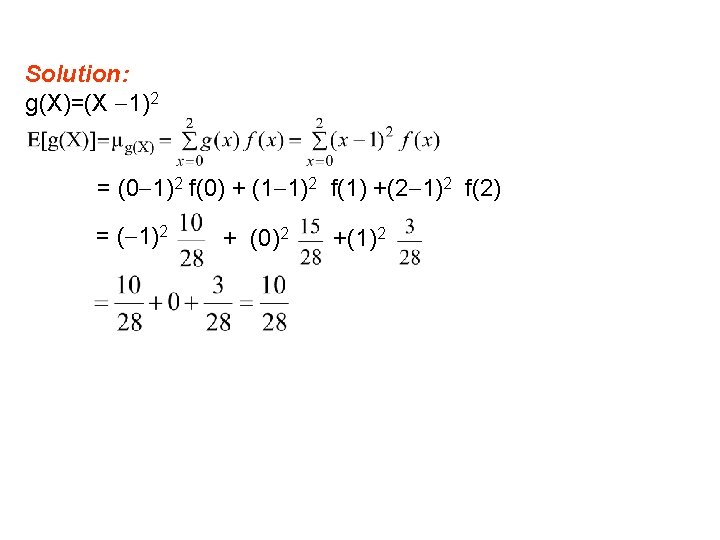



Chapter 4 Mathematical Expectation 4 1 Mean Of



Find The Intervals In Which The Function F X X 1 3 X 2 2 Is Sarthaks Econnect Largest Online Education Community



Grenzwerte Rechnerisch Bestimmen Matheretter




Rational Functions Algebra And Trigonometry




Quadratische Funktionen Parabel 1 5 Aufgaben Fit In Mathe
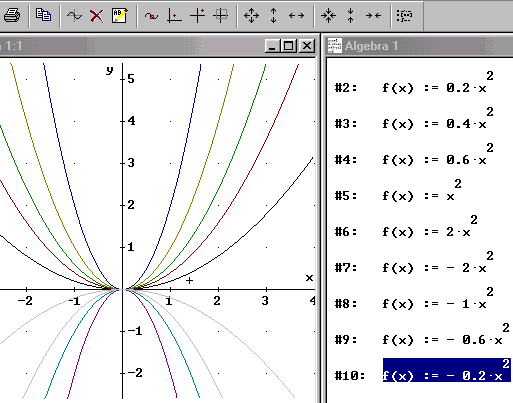



Parabelscharen Mit Derive



Gegeben Ist Die Funktion F X 1 3x 3 X 2 Nullstellen Mathelounge




If F X 2f 1 X X 2 2 X R Then F X Is Given By




F X 2 X F X 1 Exponentialfunktion Zur Basis A Fur Alle Exponentialfunktionen Gelten Die Gleichungen 1 A X A Y A X Y 2 Ax A Y Ax Y Pdf Kostenfreier Download




Naszkicuj Wykres Funkcji F Gdy A F X 1 2 X 2 X 4 B F X 2x X 1 Brainly Pl



2




Find Domain And Range Of F X X 1 X 2



2




Misc 15 Let F X X2 X G X 2 X 1 2 1 Are F G




If F X 1 4x 2 0lt X 1 And X 2 2x 1lt X 2 Where Denotes The Greatest Integer Function Then




Schnittflachen Berechnen F X 1 2 X 2 Und G X 1 3 X 3 X 2 4x Computer Schule Mathe




Nullstellen Ganzrationaler Funktionen Level 2 Blatt 1



Find F 1 If F X X 1 2x 2 7x 5 When X 1 F X 1 3 When X 1 Sarthaks Econnect Largest Online Education Community



Www Math Kit Edu Iana1 Lehre Hm1etechphys09w Media Hm1 12 Loe Pdf




If F X 3 X 1 X 2 3x Find F 0



If F X 1 X 2 3x 2 Then What Is The Value Of F X Quora




Draw The Graph Of The Function F X X 1 Brainly In




Ex 1 3 6 Show F X X X 2 Is One One Find Inverse Of F



F X 1 2 X Was Ist Das Fur Eine Funktion Kann Man Die Zeichnen Mathelounge
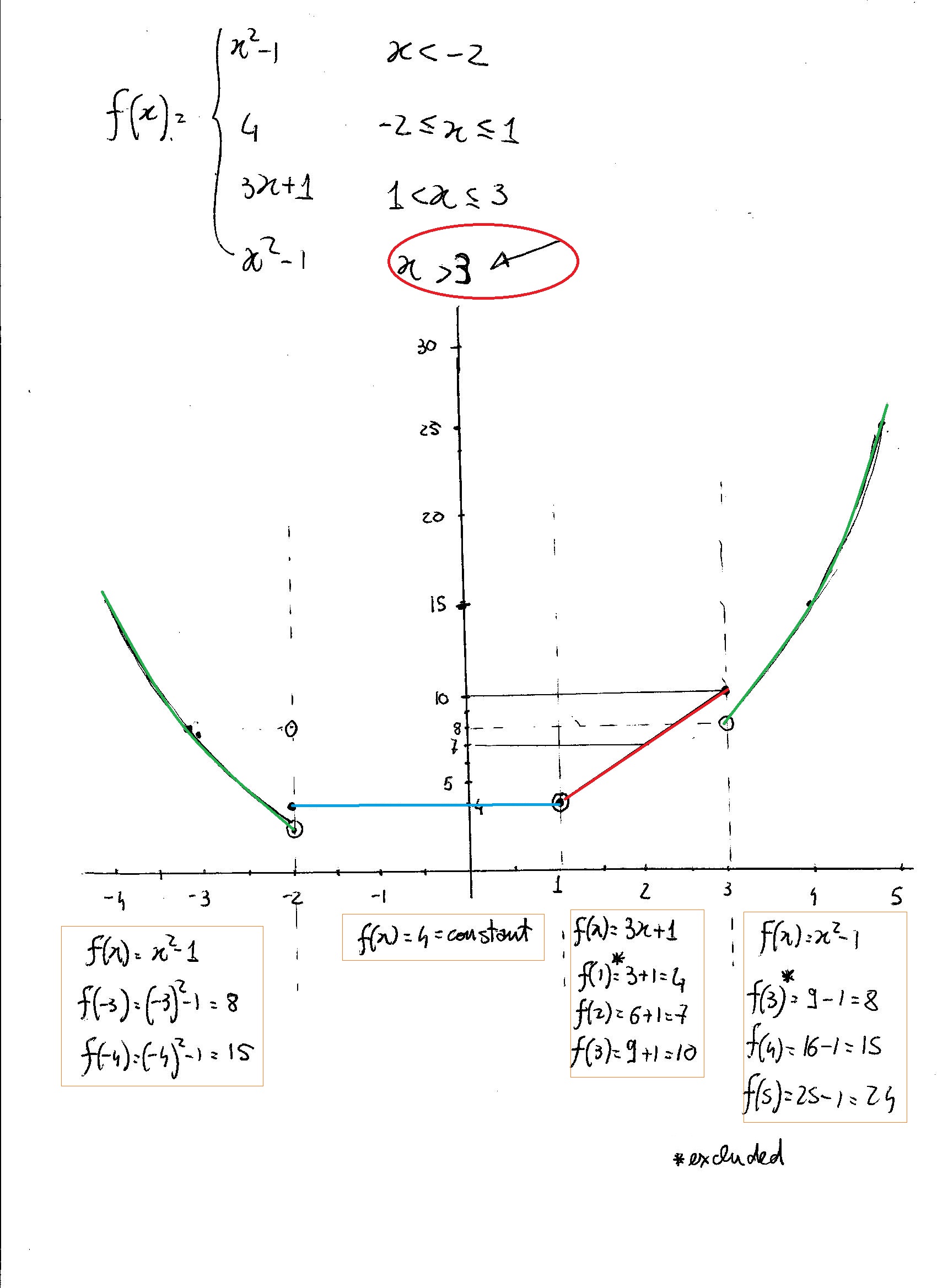



How Would You Graph F X If F X X 2 1 X 2 4 2 X 1 3x 1 1 X 3 X 2 1 X 1 How Would You Evaluate The Function At The Indicated Points F 3 F 2 F 5 F 3 Socratic




5 1 A Quadratic Function F Is A Function Of The Form F X Ax2 Bx C Where A B And C Are Real Numbers And A Not Equal To Zero




Video Ableitung Von Wurzel X Mit Kettenregel So Funktioniert Sie




Function Composition Given F X 2x 2 And G X 2 Find F ºg X F ºg X F G X Start On The Inside F G X G X 2 So Replace It F G X F 2 Ppt
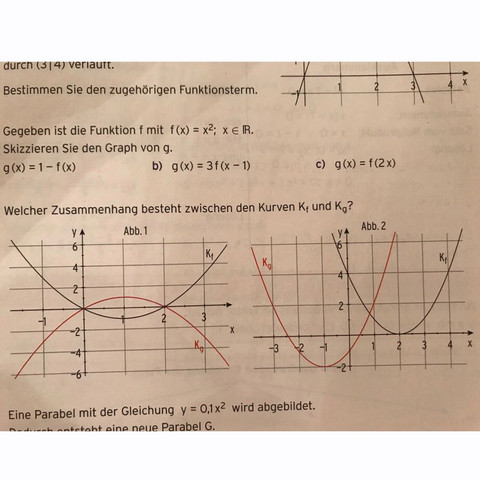



Gegeben Ist Die Funktion F Mit F X X Hoch 2 Schule Mathematik Parabel



0 件のコメント:
コメントを投稿